Fintech

上図の様に物体に入射した光は一部が反射され，一部が透過し、一部が吸収されます。

反射光の割合がＡ％とすれば、この物体の反射率はＡ％となります。同様に透過率はＢ％，吸収率はＣ％です。

ここでＡ＋Ｂ＋Ｃは必ず１００％になります。

これはエネルギー保存則（後で解説）の通りで、エネルギーは形はかえても、その量は増えも減りもしないという事で、入射光のエネルギーは（透過光エネルギー＋反射光エネルギー＋吸収されたエネルギー）になるという事です。

また放射率と言われるものがあります。これは物体がある温度になったときに、そこから光（マイクロ波～赤外線～可視光域が主）の形でエネルギーが放射されますが、この放射度合いの数値です。最も放熱し易い仮想物体が黒体で、全ての波長で放射率が100％です。現実には存在しません。

重要な点は必ず「吸収率＝放射率」の関係になることです。吸収しやすいほど放射もしやすく、吸収率がゼロであれば放射による放熱もできません。

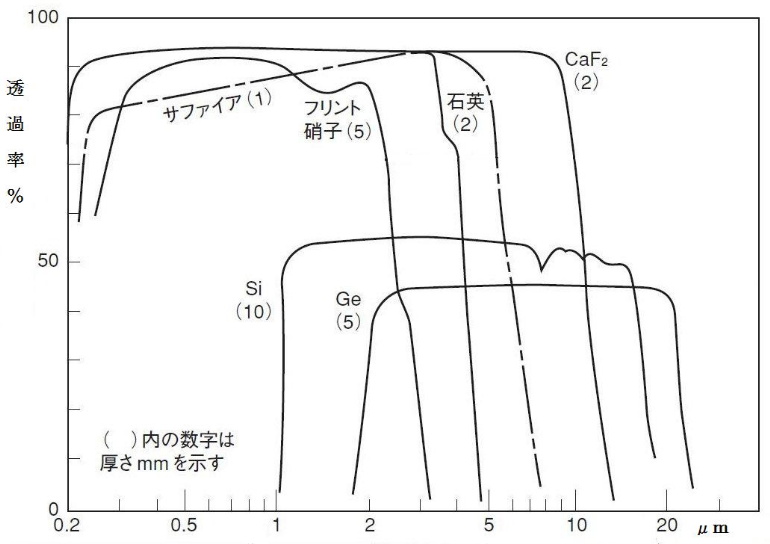
正確にはこの関係はある波長についてのみ成り立ちます。ガラスは可視光域の透過率が１００％に近く、吸収率はゼロに近いのですが、赤外域（約3μｍ以上）では透過率がほぼゼロになり、ほぼ完全な吸収体になります。温室はこの性質を利用したもので、太陽光は殆どガラスを透過して温室内に入り込み、そこで熱になって室内を温めます。温まった室内からは長波長の赤外域放射で放熱しようとしますが、その波長域ではガラスの透過率がゼロであり、このガラスの断熱性能がよければ（ペアガラスなど）熱が外部に直接出ていくことが出来ず、温室内に熱が留まります。

余談ですが、上記の話はウソではないものの正確ではありません。「地球の温室効果問題」は、地球の大気が上記ガラスと同じ効果をもつことにより、地球の地表温度が高くなる現象です。しかし温室が外気温よりも高くなるメカニズムは太陽直射光が温室の窓ガラス（又はビニール）を透過して室内を温める、までは正しいですが、室内が温まって、そこからの再放射で熱が逃げるのをガラスが止める、というのは熱量の割合的にはわずかです。現実には温まった空気をガラスやビニールで包み込むことにより外に逃げ難くして温室内温度を高く保つ、というのが主要な作用です。だから一般の温室はペアガラスまでは使わない場合がほとんどですが、それなりに温室としての効果はでます。「地球の温室効果」とは言葉は同じでも主要なメカニズムが少し違います。

放射（吸収）特性ですが、同じガラスでも温度によって特性が変化します。常温では可視光域は透明なのですが、軟化温度（１２００℃程度）になると不透明に近くなり、黄色く光る様になります。石英ガラスの場合、この温度ではまだ透明なので可視光放射率もゼロとなり、光りません。ただし赤外域では不透明なので、赤外放射はします。石英ガラスも1700℃付近から可視光域でも吸収率（＝放射率）が高くなっていくので、まぶしい白色光で光りはじめます。温度が2000℃程度のはずなのに太陽光（6000K)よりも白っぽく感じますので、青色付近に比べ赤色付近の放射率が低いのだと推定します。

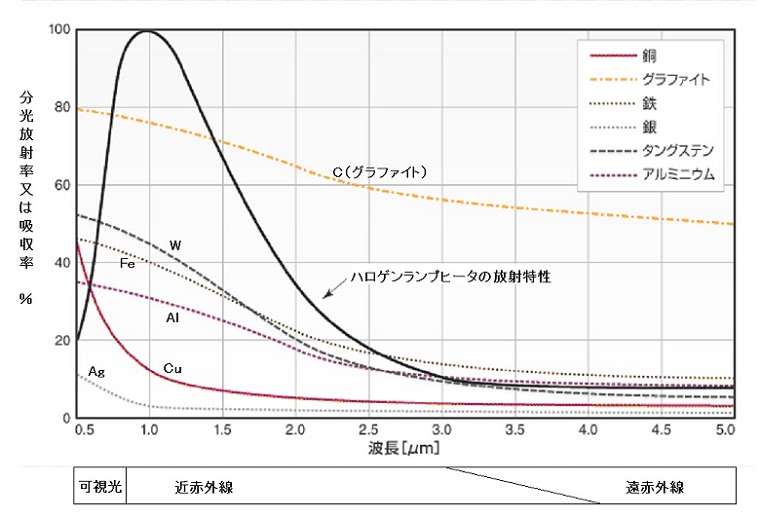
〔図－２〕は金属と非金属（セラミック，プラスチック等）の放射率（＝吸収率）の波長に対する傾向を示したものです。これは一般的傾向であり、個々の物質によって値は大幅に異なります。

　参考データ　各種物質の放射率 （吸収率と等しい）

金属は波長が長くなるほど吸収率が低下するので、遠赤ヒータでの加熱には適しません。可視光に近い波長での加熱に適していますから、ハロゲンランプヒータ（ピーク波長は約１μｍ）が最適です。それでも金属材料によっては加熱不可能に近い金属もあります。例えば銅やアルミなどは可視～近赤外域でも反射率が高く、おまけに熱伝導もよいので加熱困難です｡　ただしこれらも表面状態によっては加熱できます。（酸化変色しているとか細かい凹凸があるなど）

非金属（セラミック、プラスチック、紙、木、人体等）は一般的に上図の様に遠赤外域で放射率（＝吸収率）が高くなりますので、遠赤ヒータが適しています。ただし遠赤ヒータでは高温にはできませんので、このような対象物でも急速に高温にしたい場合などはハロゲンランプヒータの方が適しています。

放射率（＝吸収率）は１００％以上はありえません（どの波長に対しても）。仮想的な物体である「黒体」がすべての波長域で100％であり、これにかなり近いのは粉末状カーボン（９5～98％）あたりです。

人体も体温で放射する遠赤外波長域（約10μｍ）に対しては放射率９５％以上であり、極めて高いものです。もっともこの波長域では金属を除くと一般に放射率は高いですが。

ある物体がある温度になるとプランクやステファンボルツマンの式で表されるように放射という形でエネルギーが放出されます。しかし熱エネルギーが移動するのは温度差があって初めて起こります。例えば人体は非常に良い放射体ですが、周囲に対して放熱できるのは、周囲温度が体温より低い場合だけです。周囲との温度差があってはじめて放射率にそった放熱（熱移動）が起こり「涼しい」と感じます。（この場合、放射による放熱よりも対流や風による放熱の方が割合が高いのですが、ここではそれには触れません）

周囲温度と体温が同じの場合放熱出来ないというのは、温度差が無いと放射による放熱が起こらないと言ってもよいですが、周囲に対して放射したエネルギーと同じだけのエネルギーを周囲から受け取るから差引ゼロで熱移動が無いとも言えます。（後者の方が正確）

このように考えれば、どんな低温の物体からもその温度に応じた温度放射があるはずなのになぜ温かくないのか？という疑問もなくなると思います。たしかにある温度を持つ物体からは、それに応じた放射エネルギーを受けとるのですが、同時に自分からもその物体に対して自分の温度に応じた熱放射をする。自分の方が相手より温度が高ければ渡す方が多いので自分のエネルギーが減って冷たく感じる。相手の温度が自分より高ければ受けとる方が多くなり、熱エネルギーが増えて温かく感じる、という事です。この際、自分や相手側の放射率（＝吸収率）が高いほど熱移動が早くなるだけです。熱エネルギー移動の方向には全く関係しません。

ここで「自分」と表現しているのは、人体に例えると分かりやすい為そうしただけであり、どんなものに置き替えても同じことがいえます。「温かく感じる」を温度が上昇する、「冷たく（涼しく）感じる」を温度が低下する、と読み替えて下さい。

各種金属類の分光放射率(＝吸収率)とハロゲンランプ放射特性との関係

金属は一般的に可視から近赤外線域の方が吸収率が高く、これが金属類の加熱用ヒータとしてハロゲンランプヒータが使われる理由です。しかしハロゲンランプをもってしても銀や銅の光沢面は加熱が困難であろう事も、このグラフから分かると思います。

物体がある温度になると電磁波（～マイクロ波～赤外線～可視光～）の形で放射により放熱します。周囲よりも高温の物体から放熱される熱エネルギーの割合は、高温になるほど高率になり、５００℃以上ではこの放射が大勢を占める様になります。５００℃以下では対流や伝導による放熱が支配的です。

放射による放熱は物体の温度をＴ〔Ｋ〕、放射率を100％とすれば

Ｐ＝5.68×10^-12 ×Ｔ⁴　[W/cm²] 　　（ステファンボルツマンの式）

ここで注意しなくてはならないのは、上記の値は特殊な状況（周囲温度が絶対零度の場合）での放射量だということです。実際には周囲温度が絶対零度ということはあり得ず、300Ｋ（27℃）前後とかの値であるのが普通です。

そこで周囲温度をＴ0［K］とした時の物体からの温度放射を表す様にステファンボルツマンの式を一般的な形にしたものが下式です。周囲温度というのは厳密には定義が難しく、この式も近似式だと思ってください。

Ｐ＝5.68×10^-12×（Ｔ⁴　-Ｔ0⁴　）　　[W/cm²]

この式から分かるのは、物体温度と周囲温度の差がゼロであれば、温度放射エネルギーもゼロになります。周囲温度よりも物体の温度が低ければ式の値はマイナスとなります。これは物体に熱エネルギーが流入する事を意味します。

最初のステファンボルツマンの法則による放射式がまちがっているわけではありません。ある温度の物体からは［図－３］の放射が出ており、常温でも約300Ｋの絶対温度に相当する放射が出ています。ただし周囲温度が絶対零度でない限り、周囲からの温度放射を受けます。周囲温度が物体の温度と同じであれば差し引きゼロとなり、物体からのエネルギーの出入りは無くなります。

また（放射は温度の４乗に比例するため）物体の温度が周囲温度に比べて十分に高ければ、物体からの温度放射量は周囲温度の影響がほとんど無視できます。しかし物体温度と周囲温度の差が小さくなると周囲温度の影響は多大なものになります。

物体の温度に対する放熱量の実測データ

以下は実際のある物体の表面温度と、そこからの放熱量の実測データです。（室温は25℃）

物体とはφ1の鉄－クロム－アルミ線を十分な長さで外径φ23.5になるように密着巻きし、十分に酸化させたもので黒っぽい外観をしています。放射率は0.75～0.8程度と推定され、ステンレスの酸化面とほぼ同程度の放射率をもち、実際の多くのワークに近い放熱特性であろうと思います。ただしセラミックや光沢のある金属などのワークでは放熱量がもっと低い値になるでしょう。

物体の温度に対する放熱量は狭い温度範囲で大まかに言えば下式で表されます。

Ｐ≒ｋＴ^ｎ
Ｐ：放熱量［w/cm²］
ｋ：定数
Ｔ：物体の温度［℃］→正確には周囲との温度差δT

この関係を実測し、まとめたのが下のグラフです。ただし指数ｎは一定ではなく、下図の青曲線のように温度とともに変化します。これは放熱が伝導,対流,放射を合わせた形で行われ、それぞれのｎは伝導がほぼｎ＝１,対流がほぼｎ＝２,放射がほぼｎ＝４となります。温度が低いほど熱伝導が支配的で、温度上昇とともに対流による放熱が増加していき、200℃～300℃あたりから急激に放射の割合が増加していき、500℃以上ではこの放射が支配的になります。そして数千℃以上では放射がほとんどを占める様になります。つまり高温域では指数ｎは4に近づいていきます。

発熱体としてはφ29の石英管ヒータを使用した。
温度測定は700℃以上は光高温計（CHINO IR-U）を使用。700℃以下は熱電対φ0.32を使用したが、熱電対は一般的に温度が低めに測定される（測定点が熱電対線自身で冷却されるため）ので、700℃以上での光高温計の値と比較し、そこでの測定温度の両者比率が700℃以下でも適用できるとして低温域での熱電対の測定値を補正した。
この補正値は＋12％であった。この事より、物体の表面温度測定に熱電対φ0.32を使用した場合には約12％低めに測定されると推定する。熱電対での温度測定にはこの点を注意しなくてはならない。電熱線コイル内に熱電対を入れるという方法もあるが、この場合は逆に真の表面温度よりも測定値が高めにでるだろう。

物体の温度が上昇していくと、上図の様に急激に放熱が増加していきます。

その物体を目的の温度に保つ為には、その温度における温度放射その他の放熱量と同じだけの熱エネルギーを与え続ける必要があります。

例えば空中に保持された薄い板を加熱する場合、その放熱面積は表裏で計算しなくてはなりません。1400℃での温度放射は約 44[W/cm2]ですが、裏面を加えると約 88[W/cm2]の放熱となります。

しかしこれは放射率が100 ％の場合（カーボンの板などが、これに近い）であり、実際の鉄板などは酸化面の場合でも放射率80％程度なので［図－３］の値よりも実際の放熱は少ないと言う事になります。

ただし放熱は放射によるものだけではなく伝導，対流その他による放熱も加わりますから、少なくとも上図の値程度で考えておいた方がよく、実際にはもっと放熱が大きい場合が少なくありません。尚、1200℃以下の場合は［図－４］に実測データがありますので、この値を使ってください。

つまりスポットヒータなどで1400℃に加熱しようと思えば、約 90[W/cm2]程度以上のエネルギー密度を与える事になります。ただしここでも吸収率（＝放射率）を考慮しなくてはならず、吸収率８０％とすれば約110[W/cm2]程度に集光された光で加熱する必要があります。

そしてハロゲンランプを使ったスポットヒータの場合、約110[W/cm2]程度のパワー密度が限界に近く、従って加熱できる温度の上限も1400℃程度が１つの限界になります。しかし小電力のスポットヒータになるほど放射以外の伝導，対流による放熱の割合が大きくなり、例えば150 ｗタイプでは1000℃程度までしか加熱できないのが実情です。ただし２個のスポットヒータを対向させて配置し、加熱対象の表裏から加熱するようにすれば、上限はもう少し高くなります。

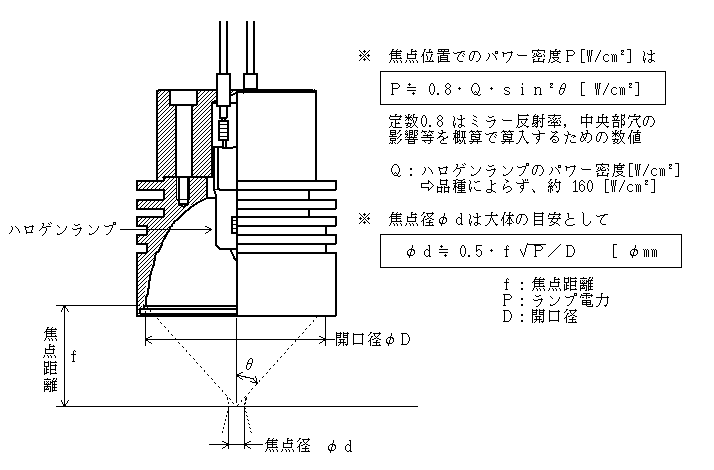
標準的なスポットヒータ用楕円鏡であるＦ値（ｆ／Ｄ）が 0.5 の場合、焦点位置でのパワー密度は
Ｐ≒0.8・Ｑ・ sin² θ[W/cm²] Ｑ≒ 160 [W/cm²] より約 64 [W/cm²]

ヒーターから主に近赤外線が出るか、遠赤外線が出るかは、その素材ではなく発熱体の温度でほぼ決まります。放射される電磁波のピーク波長λｍは発熱体の温度をＴ℃とすれば

　ピーク波長　λｍ＝　２８９６／（Ｔ＋２７３）　μｍ　　ウィーンの式　　

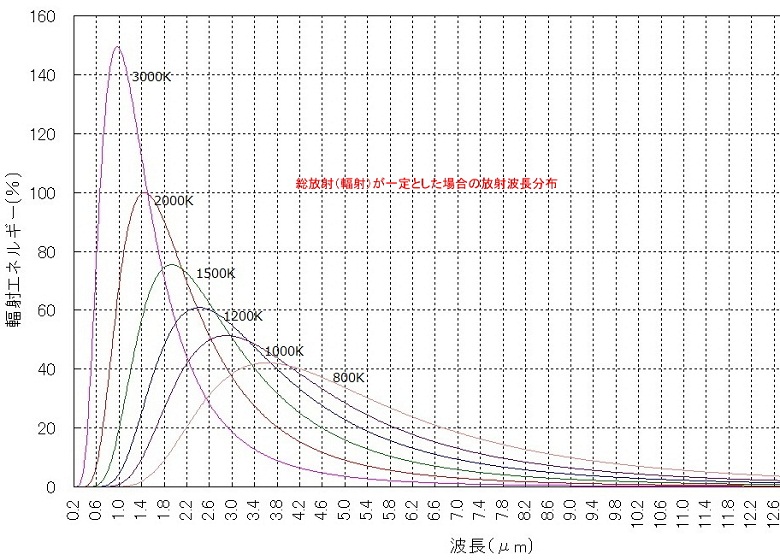
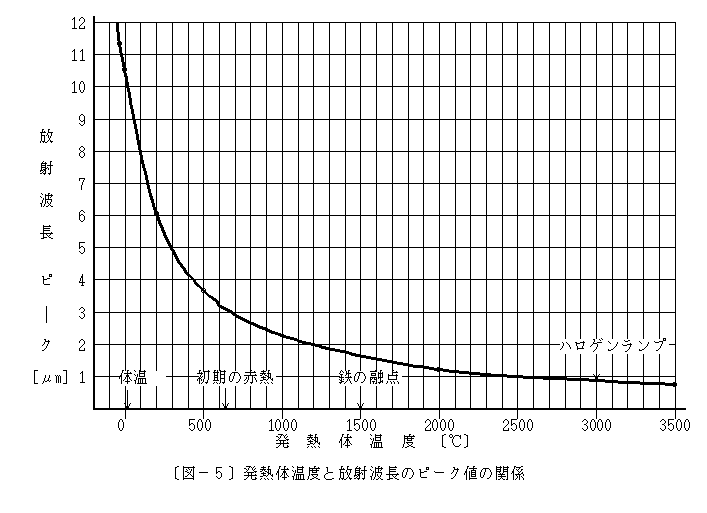
上式より各温度での放射波長のピークを求めると〔図－５〕の様になります。この放射波長をピークとして短波長側にも長波長側にも幅広く分布します。短波長側はピーク波長の1/3程度までですが、長波長側は５倍程度まで出ています。もちろんプランクの式を見れば分かるように実際にはもっと広い範囲で分布していますが、数値が極端に小さくなるので、ほとんど意味はありません。有効なのはピーク波長の 0.5～３倍程度でしょう。→下図参照

物体の温度と色

上図の温度単位［Ｋ］は絶対温度。これから273を引くと摂氏［℃］になります。300［Ｋ］のグラフが常温27℃であり、人体からの放射（体温）はこれに近い。3000［Ｋ］のグラフがハロゲンランプの放射に相当します。

放射強度は対数目盛なのでピーク位置より１目盛下がると1/10になり、２目盛下では1/100になります。従って実質的に意味のある放射範囲はピークから１目盛下程度までの範囲です。

上図から解る様に高温度の発熱体から長波長の放射が無いわけではありません。むしろ長波長の放射も高温ほど多くなります。ただ割合が少ないだけです。

放射強度が上図グラフの値を超える事はあり得ません。すべての波長域で放射率が100％の時（黒体）で上図の値となり、現実の物質は放射率が必ず100％未満なので、上図グラフよりも全ての波長で低くなります。また現実の物質は放射率の波長依存が一定ではないので、上図グラフの山の形と全く相似形というわけでもないですが、基本的にはほぼ上図グラフの形となり、物体の組成などによる差は僅かです。

上記した「温度放射強度と波長分布」は以下で説明するように「プランクの法則」により求められますが、計算はかなり面倒なので実用上は上記グラフを利用するだけでもよいと思います。

黒体における単位面積・単位波長あたりの放射エネルギー密度 W (λ,T)は

W(λ,T) = 8πhc/λ⁵/( exp( hc/λkT ) -1)　［w/m²]

λ：波長［m］
Ｔ：黒体の温度[K]
ｃ：光速　3×10⁸　[m/s]
ｋ：ボルツマン定数1.3807×10^-23　[J/K]
ｈ：プランク定数 6.626×10^{-34　[J・s]}

以下は「温度放射強度と波長分布」のもう少し細かく見やすい資料です。放射強度の単位が先の資料とは違い、単位立体角当たりの放射［w/cm^2/sr/μｍ］になっていますので、平面からの総放射に直すには×2πする必要があります。

単位面積あたりの放射絶対量

可視光は約 0.4～0.8μｍの範囲です。約 0.4μｍ以下を紫外線と呼び、0.8μｍ以上を赤外線と呼んでいます。約 ４μｍ以上を遠赤外線、それ以下を近赤外線と分類する場合がありますが、この分類にさほど大した意味はありません。光が熱に変わるメカニズムも同じです。赤外線には熱に変わる事以外の働きは全くありません。

ハロゲンランプの放射特性（計算予想値）

赤線グラフは比較のための2600Ｋ黒体放射）

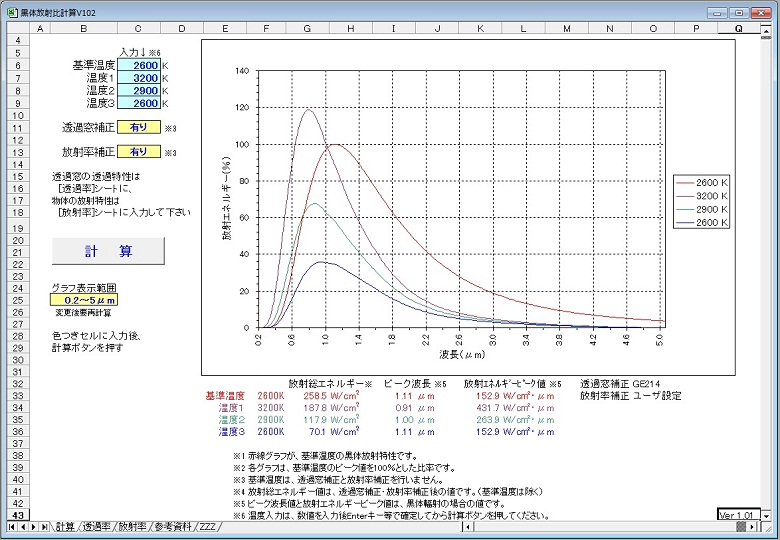
グラフの赤線は2600Kの黒体放射です。(温度１)は3200Kのハロゲンランプ（寿命200時間）のものです。
(温度２)は2900K（寿命2000時間）のものです。温度３は2600K（寿命5000時間以上）のものです。これらは黒体放射にタングステンの放射率特性と石英ガラスバルブの透過特性を反映させたものです。主にタングステン（発光体材料）の放射率特性により同温度の黒体放射よりも総放射で1/3以下となります。
また長波長ほど放射率が下がるというタングステンの特性と、約４μｍ以上の波長を透さないという石英ガラスの特性により、４μｍ以上の波長はほぼゼロとなっています。
上図を作成したソフトウェアは弊社で販売しています。⇒温度放射の計算

黒体放射

総放射量が一定とした場合。単位面積あたりの放射絶対量はこちら

各種透明体とシリコン，ゲルマニウムの透過特性の例

下図は光学材料やシリコン，ゲルマニウムの分光透過特性です。
石英ガラスでも透過率は93％程度ですが、これは反射が7％ほどあるためです。石英ガラスは可視光域での吸収はほとんどありません。他の材料も７％程度は反射分がありますので、吸収率はそれを差し引いて考える必要があります。純粋な石英ガラスは通信用光ファイバーとして使われています。これは数十kmも光信号を送れるほど完全に近い透明体です。

ここでは温度放射を利用した赤外線ヒータについてのみ解説します。温度放射とは物質を高温にしたときに、そこから放射される電磁波（広い意味での光）です。温度放射以外の光加熱方法としてはレーザー加熱などがあります。

近赤外線ヒータとは一般的に電球（ハロゲンランプ）であり、2000～2800℃程度の発熱体から放射される光を利用します。ピーク波長は約１μｍ（0.001mm ）であり、0.5～3μｍ 程度の範囲に分布します。これは可視光をかなり含みますので、一般的にまぶしい。これについてはガラスに着色するなどの方法で可視光を減じる対策方法もあります。また発熱体温度を2000℃程度またはそれ以下に設定すれば、さほどまぶしくはありません。

遠赤外線ヒータとはセラミック，石英，金属酸化面などの比較的低温（ 500℃～1000℃)の発熱体から放射される光を利用します。ピーク波長は３～５μｍであり、１～１５μｍ程度の範囲に分布します。かすかに赤熱する程度であり可視光はほとんど含まないので、まぶしくありません。

赤外線加熱を採用される場合には以下の様な赤外線の性質を考慮して、遠赤外線ヒータを使うか近赤外線ヒータを使うかの選択をしなくてはなりません。

遠赤外線はほとんどの物体を透過しないため、ごく表面（0.1～0.2mm）の加熱になります。そのため接着剤の加熱に遠赤外線ヒータを使った例では、たとえそれが透明に近い接着剤でも表面が焼け、内部まではなかなか熱が伝わりません。近赤外線ヒータの場合には浸透（透過）して内部からも加熱されるため、内部から泡が出てきます。そのため、接着剤加熱用にはこの近赤外線ヒータでなくてはならないとされています。

印刷した紙を加熱すると、遠赤外線ヒータの場合には全体的に加熱されます。近赤外線ヒータの場合には印刷文字や写真の部分が強く加熱されて白紙の部分はあまり加熱されません。つまり近赤外線は被加熱物の表面状態（色など）により吸収されやすさの差が大きい、つまり加熱度合いにムラが出やすい傾向があります。

例えば近赤外線ヒータで肉を焼くと、焦げ始めたところが黒くなるので近赤外線をよりよく吸収するようになり、さらにその部分が集中的に加熱されるという循環がおこり、局部的に強く焦げます。つまり同じ素材でも焦げ目がムラになりやすい。遠赤外線ヒータのほうが均等に焦げ目がつきます。

これはデメリットでもありますが、目的によってはメリットにもなります。例えば部分的に加熱したい場合には加熱したい部分だけを黒く塗装しておけば良い、などです。

近赤外線ヒータは通常、通電開始後１秒間程度で使えますが、遠赤外線ヒータは３０秒～数分間かかります。

供給電力の放射エネルギーへの変換効率は、近赤外線ヒータでは９０％程度となり良好です。遠赤外線ヒータの場合は６０～７０％程度でかなり悪くなります。赤外線にならなかったロスエネルギーは主に空気を温めます。

近赤外線ヒータ（ランプ）から出る可視光線は加熱に寄与しない、と勘違いされている人がいますが、可視光も吸収された光エネルギーは全て熱に変わります。

近赤外線は木材，紙，布，人体などの比較的淡色の物体に対しては一般的に吸収率が遠赤外線よりも悪くなりますが、ヒーター自身の変換効率を考慮すると差は少なくなり、更にヒータ自身の立ち上がりに要するエネルギーと時間のロスも考慮すると必ずしも遠赤外線ヒータの方が効率が良いとは限らず、むしろ近赤外線（ランプヒータ）の方がエネルギー効率が良い場合が多いです。

更に高反射材で閉鎖空間を作りその中で加熱する場合、高い総合熱効率が期待できます。これは最初の照射で吸収されずに反射された光も壁面で再反射され、また被加熱物体に当たり再吸収されるという事を繰り返すために、高い吸収率となるものです。この場合の総合熱効率ηは壁面の面積をＳ1，吸収率をD1とし、被加熱物体の表面積をＳ2，吸収率をD2とすれば

　　効率η≒S2×D2/(D1×S1+D2×S2)×(ヒータの変換効率)

閉鎖空間とまではいかなくても、大きな反射板で被加熱物体を覆う様な場合には、上記に近い状況となり、高い総合熱効率になります。

ヒータの発熱体から放射されるエネルギー密度は近赤外線ヒータが高く遠赤外線ヒータは低い。その差は20～40倍にもなります。集光ミラーで赤外線を一点に集めても発熱体の表面エネルギー密度以上には原理的に決してならないので、遠赤外線ヒータではあまり高いエネルギー密度は与えられません。(遠赤外線ヒータは数w/cm^2程度。近赤外のランプヒータは100w/cm^2以上)

したがって遠赤外線では急速加熱や高温加熱，スポット加熱は難しく、このような用途では近赤外線ヒータが適しています。工業用では加工速度やエネルギーコストが重視されるために、ほとんどの場合、急速加熱が求められ、工業用加熱に関しては近赤外ヒータ（ランプヒータ）が有利です。

急速に加熱してかまわない場合には、できるだけ高いエネルギー密度を与えて短時間で急激に温度上昇させた方が電力消費効率が非常に良くなります。低いエネルギー密度で長時間をかけて温度上昇させる場合、目標温度に達するまでの被加熱物体からの放熱がロスとなるためです。急速加熱と低速加熱では必要電力量が数倍になることもあります。

近赤外線加熱（ランプヒータ）は遠赤外線ヒータの数十倍のエネルギー密度を与える事が可能なので、このような場合には高いエネルギー効率が期待できます。目標温度に達したら必要に応じて電源を切ったり、パワーを下げて目標温度をキープするようにコントロールしたりします。

ただし大きなエネルギー密度を与えて急激に加熱するのは、被加熱物の種類によっては適さない場合もあります。例えば厚肉の食材などを加熱する場合には表面だけが焼けて内部の温度が十分には上がっていない、ということもあります。このような場合には低いエネルギー密度で長時間かける必要があります。

遠赤外線加熱の場合にはもともとエネルギー密度が低いので、必然的に加熱に長時間かかるので内部まで熱が伝わりやすいのですが、近赤外線ヒータでは場合によってはエネルギー密度を下げるようにコントロールする必要があります。

ごく表面でしか吸収されない遠赤外線に「物体内部に浸透して内部から加熱される」などという誤解が生れたのは、エネルギー密度が低くて加熱に時間がかかったのが原因と思われます。

弊社の実績的には多くの場合、近赤外線ヒータの方がよい結果が出ますので、実験や経験により判断されて遠赤ヒータを近赤ヒータに交換される事例は多く存在します。簡単な実験でわかることですから、まずやってみてください。

遠赤外線には嘘や誤解が多くあります → 参考　遠赤外線の嘘の宣伝について

光（赤外線含む）の反射という現象は大別して次の２つの形があります。

①金属面による反射：自由電子の働きによる反射。反射の法則にそった指向性の強い反射となる。
②微小透明体による反射：白紙や白布，小麦粉などの反射。通常は拡散反射（乱反射）となる。

①の金属面による反射はごく表面で行われる。反射の法則どおりに反射するので、乱反射させるには表面を凹凸にする必要がある。しかしこれを行うと反射率が低下する場合が多い。金属を細かい繊維状や粉末にすると、乱反射してその金属面間で何回も反射を繰り返す事が多くなり、そうなると吸収量が多くなる。

例えば反射率０.９のアルミ面でも５回反射すると（0.9）5＝0.59となる。金属を細かくするほど表面の曲率が小さくなり、反射して外部にでるまでにその粉末や繊維内で反射を何度も繰り返すので、反射率が小さくなり、黒っぽくなっていく。

金属面での反射には自由電子の働きが大きく関与するため、一般的に電気伝導度のよい材料が反射率もよい傾向があります。例えば電気伝導度のよい材料は銀，金，銅，アルミなどですが、これらは優秀な反射材料です。金，銅は可視光の短波長域で反射率が落ちるので着色し、可視光反射率が若干劣りますが、赤外域では優秀な反射率を持ちます。

光加熱スポットヒータなどで金メッキミラーを使うのは赤外域反射率が最も優秀なためです。銅も優秀なのですが、酸化などにより劣化しやすいので使いません。銀も空気中の硫黄化物などにより黒く変色しやすいという欠点があります。

余談ですが、熱の移動にも自由電子の働きが大きく関与します。そのため電気伝導率の優秀な材料は熱伝導率も優秀です。（銀，銅，金，アルミニウム等）

上図からハロゲンランプの放射エネルギーを利用するという目的では金メッキ鏡が優れているのが分かります。アルミ鏡は反射効率が金メッキ鏡に比べ約10％落ちます。ただし可視光用としては短波長側（青領域）の反射率が悪く、着色するので使えません。紫外線用としてもダメです。このような短波長領域や可視光全域用ミラーとしてはアルミが適しています。

金属面での反射に対して②の反射は逆の傾向があります。例えば氷砂糖は透明であり、ほとんど光を反射しない。空気と氷砂糖の屈折率の差による僅かな境界面反射だけです。しかしこれを細かくしていくと微小粒の内部で光が複雑に屈折，反射して、そのうち元に戻される光が増えてくる。

ザラメはそうでもないがグラニュー糖くらいになるとかなり反射されて白っぽくなり、白糖になるとかなり高い反射率となり真っ白な拡散反射（乱反射）をする。水の結晶（氷）でも同様。氷の固まりは透明だが、これの細かい結晶である雪は真っ白で高い反射率となる。

白い布や紙も顕微鏡で見ると透明な繊維で構成されている事がわかる。白い紙の反射原理は上記砂糖や氷の例と同じであり、透明な細い繊維を光が通過するときに複雑に屈折し、一部は境界面で反射され、それが繊維の中で何度も繰り返される事で逆戻りする光が増え、高い反射率となる。

つまり金属以外で反射率の高い材料というのは素材としては透明体であり、しかもそれが細かい粉末状や繊維状になることで、その内部で複雑な屈折，界面反射を繰り返して入射光が乱反射される。反射率は素材の透明度が高いほど、また屈折率が高いほど高くなる。従ってこれらは金属の様な指向性の強い反射はしない。

白紙や白布を構成する繊維素材の光の透過率は可視光～近赤外線では良好だが（透明度が高い）遠赤外域になるほど一般的に不透明になっていくため、反射も起こりにくくなる。白紙や白い布，白い顔料などの加熱に遠赤外線ヒータが適しているのは、このような原理で反射光や透過光が減り吸収率が高くなるためです。

余談　上記以外の原理による反射

透明体材料による反射は拡散反射になると説明しましたが、透明体でも金属面のような鏡面反射をする場合があります。例えば薄いガラスの板は空気との界面で数％の鏡面反射をします。これだけならわずかな反射量なのですが、この薄いガラス板を何枚も重ねると反射が加算されて全体として高い反射率を示すようになります。

このように薄い透明膜をたくさん重ねる事により金属光沢をもっている自然界のものとして、例えば魚の鱗があります。また昆虫類にもこの原理により金属光沢を持ったものが存在します。

工業的にも薄膜を多数重ねる事により反射鏡として利用する技術は各種の分野に利用されています。これらは高屈折率の薄膜と低屈折率の薄膜を交互に塗り重ねます。１５層程度で金属反射鏡に匹敵する反射率となり、２１層では金属反射鏡よりはるかに高い反射率が得られます。屈折率の差が大きいほど高い反射率が得られるので、高屈折率の材料としては二酸化チタン、低屈折率の材料としては酸化マグネシウム，二酸化ケイ素（高耐熱）などがよく使われます。

このような多層膜反射鏡は高い反射率が得られるだけでなく、膜厚をコントロールすることにより波長によって選択的に反射させたり透過させたりできます。これは光の干渉という現象を利用するもので、さまざまな利用分野があります。 (膜厚が1/2波長となる波長付近は反射しなくなり透過する）

例えば可視光線は反射して赤外線は透過させるような選択反射膜も作れます。これによりランプからでる赤外線を含んだ光の中から必要な可視光だけを取り出し、照明には不要な（照射物の温度上昇を招き、不都合）赤外線を除去できます（クールビームランプ）。また特定の波長帯のみ反射する膜で白色光を光の三原色に分ける事も可能です。ビデオカメラ，ビデオプロジェクターなど光学機械にはこの技術がよく使われています。

人間の目の見える波長域（可視域）と太陽光の波長分布は、そのピークがほぼ一致します。これはもちろん偶然ではなく、人間が太陽光を使って情報を入手し、それを武器に生存してきた結果、つまり生物進化の産物です。

赤外域や紫外域を利用しなかったのは、あまり広い波長域でレンズ（水晶体）の焦点を一致させるのは困難であり、また目に使える材質的な問題もあり、これを行なおうとするとかえって生存に不利だったからと考えられます（大きく重くなるなど）。もちろん進化の過程でこのような試行錯誤も行われたはずであり今後も行われるでしょう。他の生物では人間の可視範囲とは必ずしも一致しません。超小型の目には短波長の方が好都合とも考えられます。昆虫類の目の感度は短波長側にずれており紫外域（ＵＶ）まで見えます。

上図からもわかるように、太陽光には遠赤外線はほとんど含まれません。太陽光の加熱効果は可視域の光～近赤外線によるものです。可視光も当然の事ながら加熱作用があります→吸収された光エネルギーは波長に関係なくほぼ全て熱に変わる。

ただし青色光～紫外線のような短波長の光の場合、光子エネルギーが大きいので吸収された光エネルギーが光化学反応で化学エネルギーにかわり蓄積されるなどの場合があるため100％熱エネルギーに変わる、とまでは言えません。ただしあったとしても割合的にはごく微量なので、全て熱に変わると思っても大きな間違いではありません。赤外線領域では光子エネルギーが小さいので光化学反応は全く起こらず、完全に100％、熱に変わります。

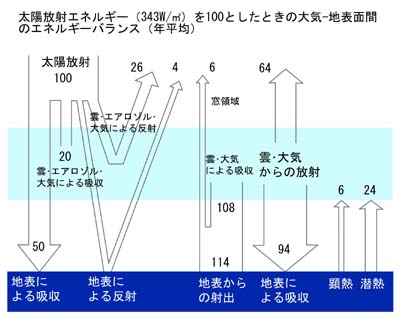
遠赤外線は元々の太陽光線がほとんど含まない上に、空気中の水分などで吸収されるため、太陽からの直射光にはほとんど含まれません。

ただし空気中の水分などが吸収する、という事は放射する、という事でもあり、大気や雲からの長波長の遠赤外線が大量に地上に降り注ぎます。上図からわかるように太陽からの直射光の２倍近いエネルギーが大気や雲からの遠赤外線放射という形で地表に降り注いでいることになります。

そして地表からも空に向かって更に多くのエネルギーが10μm付近の遠赤外線で放射されています。

これを「暖かい」と感じる事はありませんが、これがないと極端に日陰は寒く夜は冷え込む事になります。もしこれらがゼロであれば放射冷却により極限的には宇宙空間の温度（約－270℃）にまで冷却されうる事になります。