ハロゲンランプ加熱，その他放射熱応用のスポット加熱に必須の反射鏡設計に関する解説
|
目次
１．光加熱のための反射光学系についての概要
２．光源像の出来方の基本的考え方
３．微小ミラーＳが扱う光エネルギーの算出
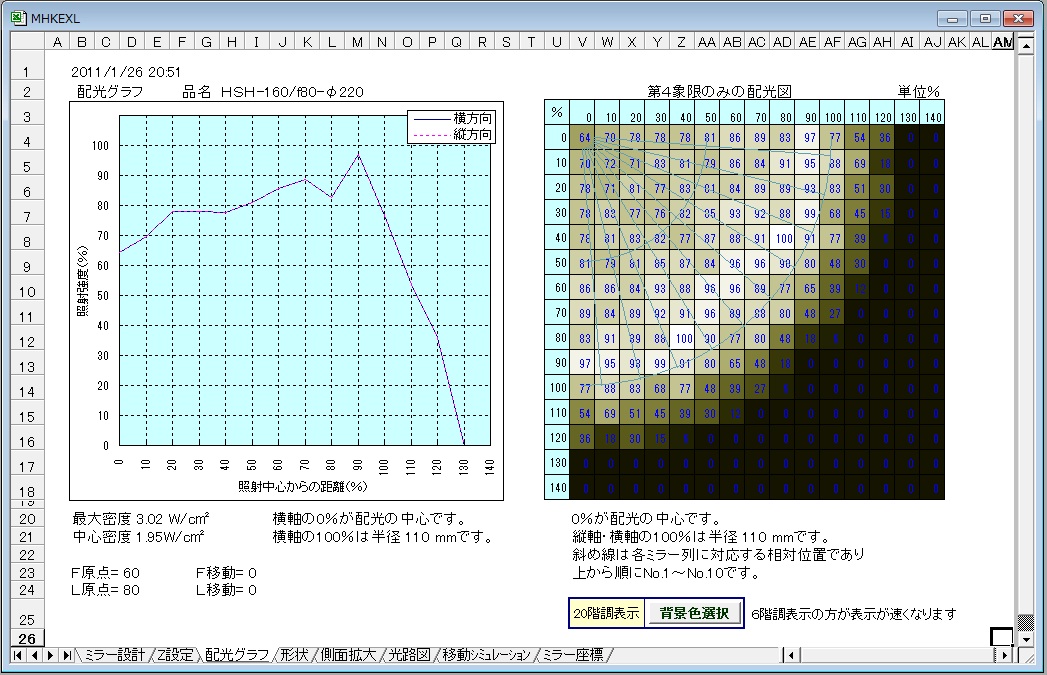
４．スクリーン上での配光分布を計算する方法
５．楕円面鏡（点集光用）による配光分布の例と考え方
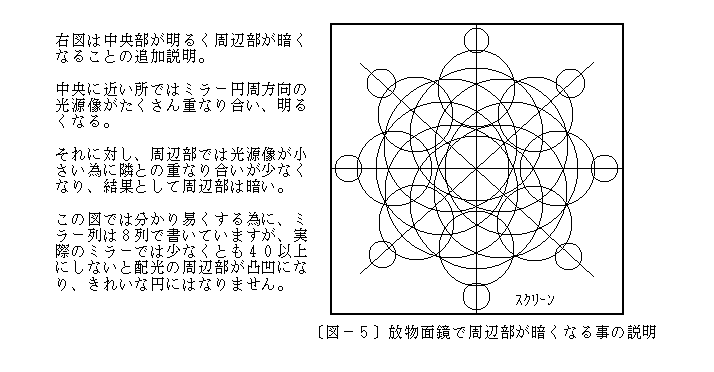
６．放物面鏡（平行光用）による配光分布の例と考え方
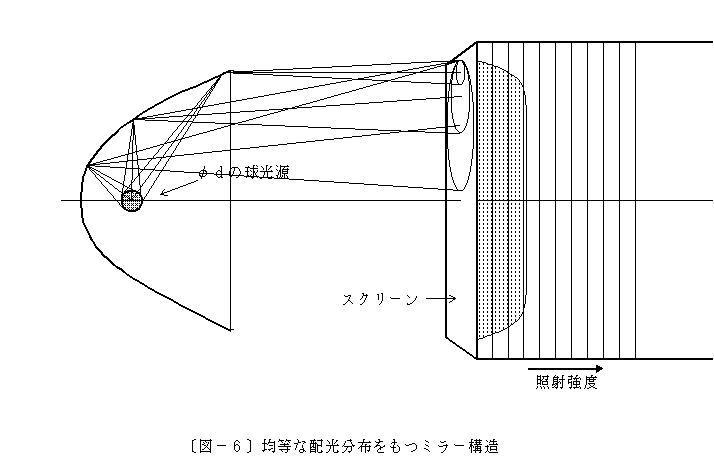
７．均等な配光分布をもつミラー構造例と考え方
８．ミラー座標の求め方
９．試作による評価
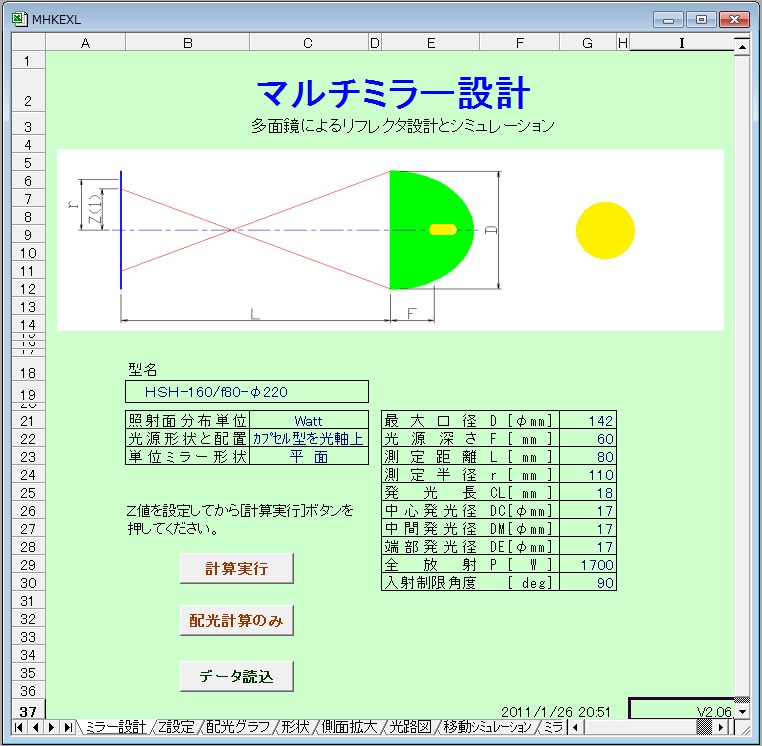
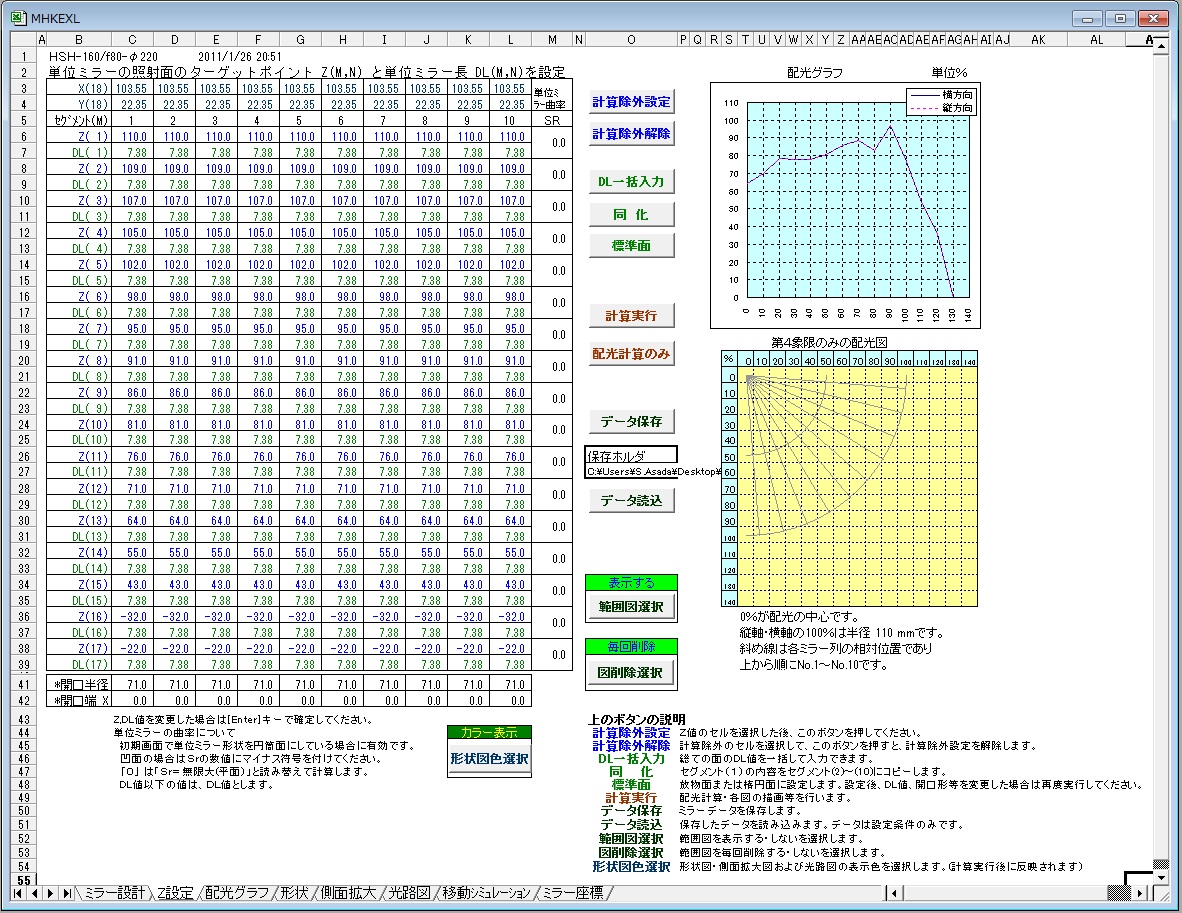
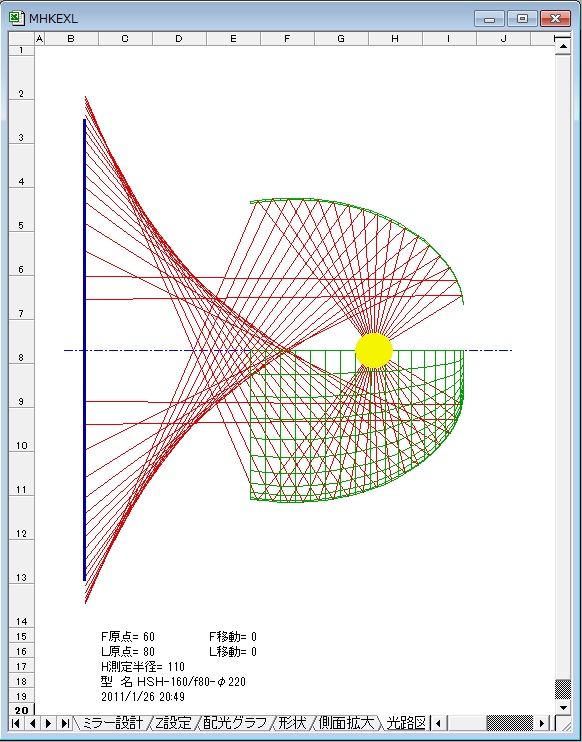
参考. パソコンソフトによる設計例
１．光加熱のための反射光学系についての概要 |
| * | ハロゲンランプによる光加熱は、レンズやミラーなどを使いハロゲンランプのフィラメント（約28００℃）の光源像を作って、それにより加熱するものです。 なお、光源像を作るという方法は最高温度を得たい場合であり、比較的広い面の照射の場合などは（単一の）光源像は作りません。 １枚のレンズでランプの光源像を作る場合はレンズ口径に対して焦点距離が比較的長いので、きれいな光源像を結びますし、配光分布がどのようになるか、パワー密度はどうか、なども比較的簡単に計算可能です。 しかしレンズのみによる光学系は光源から出た光の２０〜３０％しか利用出来ないため、加熱用にしても照明用にしても経済的ではありません。 そこで反射光学系にして、光源を覆ってしまうような深いミラーにすると７０％程度の光を利用できるようになりますので、多くは反射光学系が利用されます。 しかしこのような深い反射鏡には問題もあります。光源が点であれば話しは簡単なのですが、現実の光源には必ず面積があります。光源を覆い尽くすような深いミラーの場合、レンズの様にきれいな光源像はできません。収差が大きすぎてレンズによる光学設計方法では全く実用になりません。 以下で御紹介するのは正確な配光分布を計算により予測したり、目的の配光分布になるようなミラーを設計する方法です。尚、この方法はもしかすると光学設計のスタンダードではないかもしれませんが、基本理論が極めて単純明快なので理論的妥当性に疑問の余地がほとんどありません。また実績的にもこの設計方法で全く問題なく設計できております。 計算を単純化するには、光源を球形として扱うのが最も簡単です。そして加熱用としてミラーに組み合わせる光源は多くの場合、球形に近づけるよう縦横比を１：１に近くしますので球形光源として設計しても十分正確で実用的な配光分布が計算できます。 球形と見なせない光源については多数の球光源の集合として近似することにより、正確な配光分布が計算できます。照明用のミラーではこの手法が必要な場合もあります。多数の球光源として扱う場合は重なり部分の排除処理が必要なので、少し面倒な処理が必要です。 |
関連情報 → 光加熱の物理 シャープな配光のミラー集光系
２．光源像の出来方の基本的考え方 |
| * | ここではミラー面を多数の平面微小ミラーに分割して設計する。分割数が５００程度であれば連続面のミラーと光学性能は大差ないし、数千以上になれば、ほぼ完全に同じ。最近のコンピュータなら数万以上にしてもほとんど瞬時に計算できる。 分割数が２００程度だと、ほどよくボヤケる効果があるので、特に照明用ミラーなどでは分割数の比較的少ない多面構成のミラー（マルチミラー）がよく使われる。またこの設計方式で設計しておいて、実際の製作では作りやすい旋盤加工による回転多面体ミラーも加熱用には多用している（少量でも低コストで製作が容易なため） |
〔図−１〕光源像の出来方の基本的考え方
※設計の基本思想
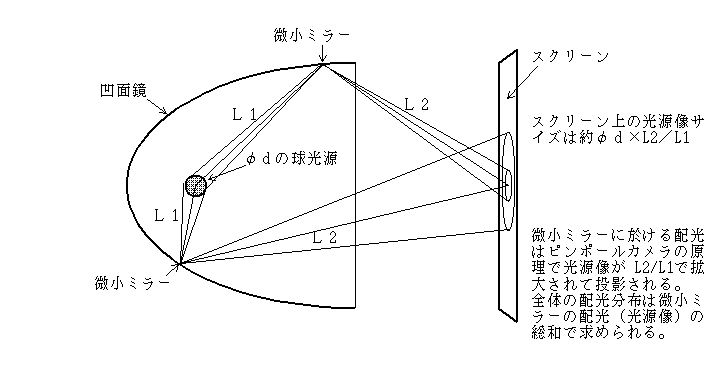
| * | 上の〔図−１〕のようにミラーの一点をとって、それを微小ミラーとして考えると、ピンホールカメラと同じ原理で光源の像がＬ２／Ｌ１で拡大されてスクリーンに投影される事になる。これからスクリーンに投影される光源の面積が求められる。 微小ミラーＳによりスクリーン上にできる光源像の径φＤ： φＤ＝φｄ×（Ｌ２／Ｌ１） 厳密には斜めに入射するのでスクリーンに投影される光源像は真円にはならず、また光源像は中心が最も照度が高く、周辺は若干暗くなるが、多少の誤差を許容するならばスクリーン上で直径がφｄ×（Ｌ２／Ｌ１）の均一照度円になるとして計算すれば処理が簡単。 本当に厳密な配光分布を求めるのであれば光源像の形，照度分布を厳密に求めれば、厳密な配光を求めることも可能。ただし当社で扱った範囲の用途では、そこまでの必要性は感じなかった。→手間＆費用対効果の点で不要と判断。 |
３．微小ミラーＳが扱う光エネルギーの算出 |
| * | 下図〔図−２〕の方法で微小ミラーＳに入射する光エネルギーが算出されるので、前記方法で算出したスクリーン上の光源像面積で割ると、この微小ミラーでスクリーン上に照射されるパワー密度[W/cm2] が算出される。（厳密には入射角度が異なるので、照射される範囲がどこも同じパワー密度というわけではないが、この誤差は通常小さいので無視する。） |
〔図−２〕微小ミラーＳが扱う光エネルギーの算出
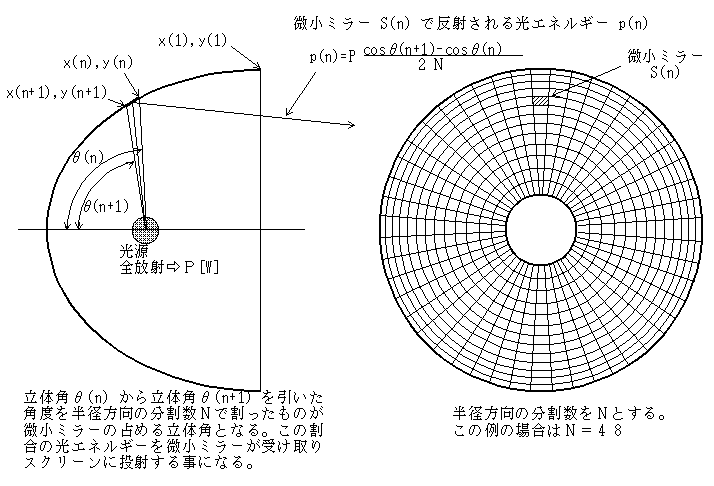
上図の微小ミラーが受け取るエネルギーｐ(n) は、光源からの総放射をＰ[w]
とすれば、全立体角
に対する微小ミラーが受け取る立体角の割合で求められる。
cosθ(n+1)
-cosθ(n)
p(n) = P ・───────────── [W]
２Ｎ
Ｎ：半径方向の分割数（上図で放射状に見える分割）
４．スクリーン上での配光分布を計算する方法 |
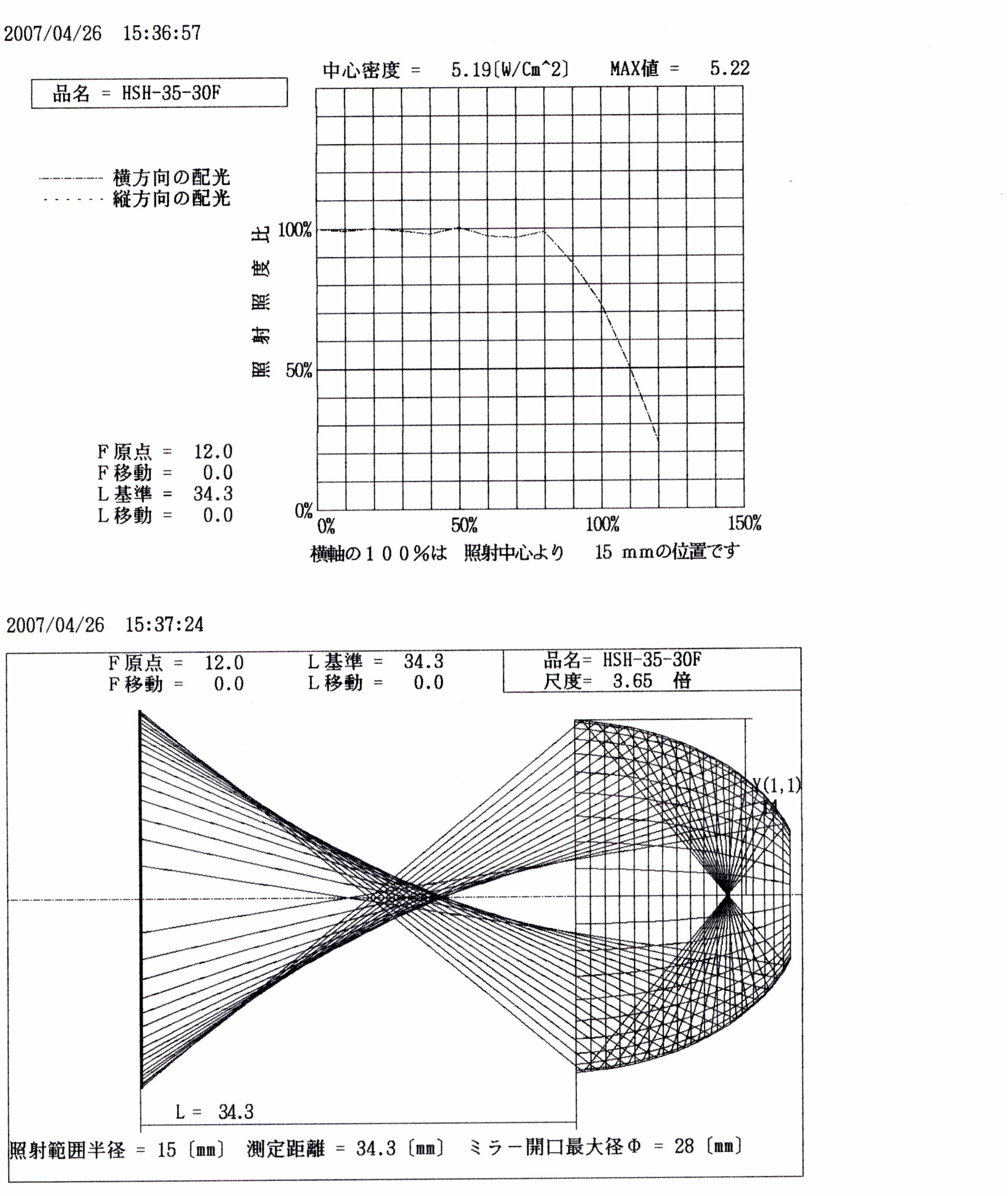
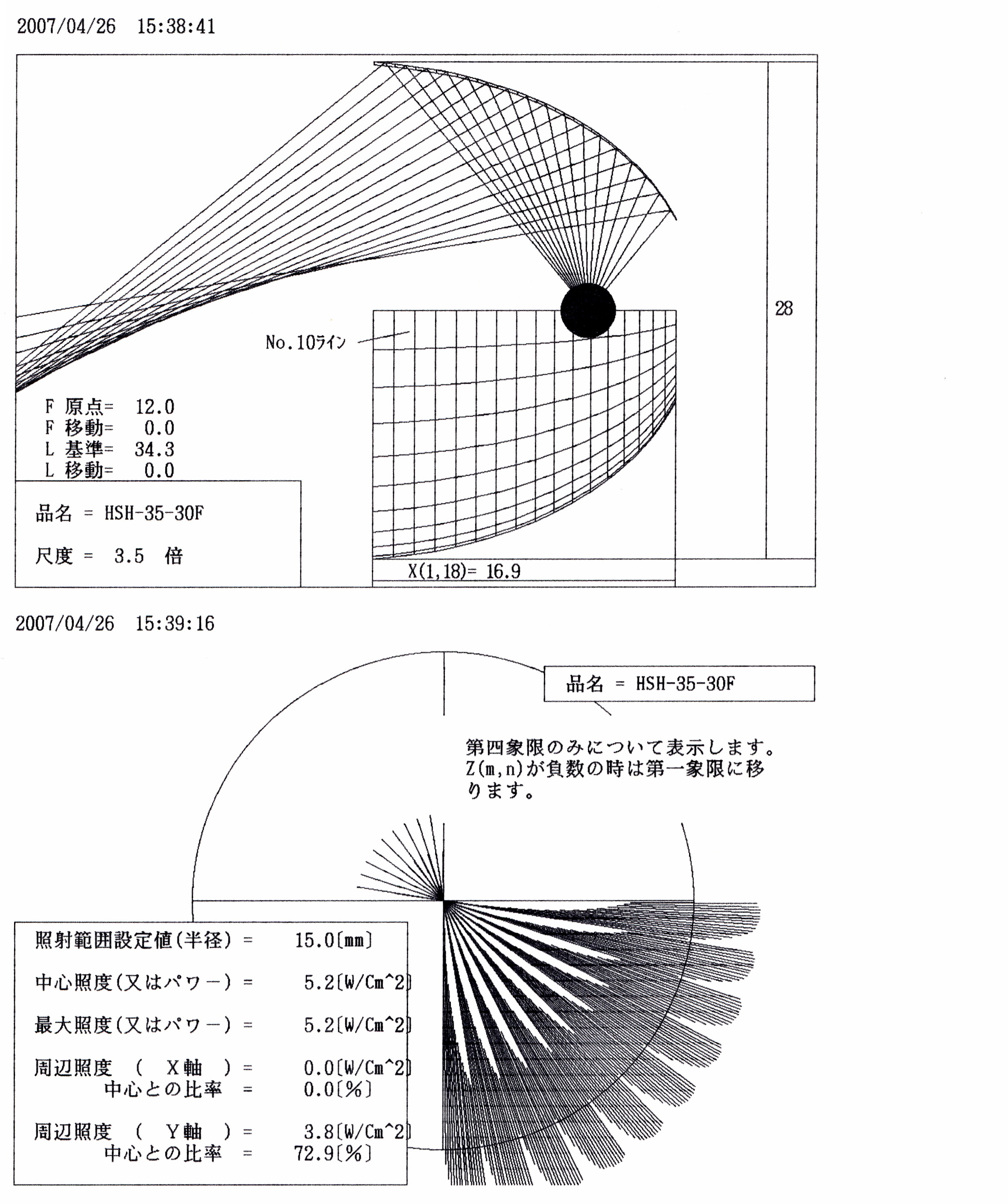
| * | スクリーン上での配光分布を評価する方法として、必要とされる精度に応じ、スクリーン上に仮想センサーを多数仮想配置する。通常は縦横２０個（計４００個）で十分。 そして微小ミラーによりスクリーン上に出来た光源像の中に、それぞれのセンサーが入っているかどうかを判断させる。もし入っていればそのセンサーにその時の照射パワー密度を加算する。この作業を全ての微小ミラーについて行なう。するとそれぞれのセンサーにそれぞれの微小ミラーからの照射パワー密度が加算されていき、全体としての照射分布データが得られる。 光源が球か、又は棒状でも光軸上に同軸で配置されていれば、そしてミラー面が歪みのない回転体ならば配光分布は単純な回転対象形になるので、センサーは面に分布させなくても中心からの一列配置で十分である。面配置が必要なのは光源が球以外の形をしているとか光軸からずれて配置されているとか、ミラーが歪んだ形をしている場合など、照射分布が複雑な形になると予想される場合のみ。 実際の場面では、面での照度分布評価が必要な場合は稀である。一列配置で大部分は間に合うし、多少複雑な配光分布のものでも中心から縦一列と横一列の配置でまにあう場合が多い。 |
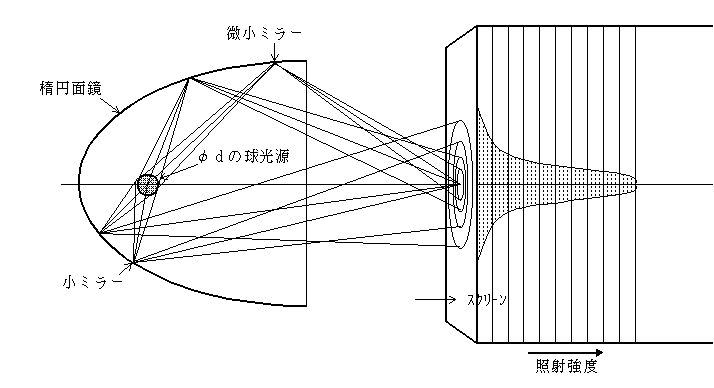
５．楕円面鏡（点集光用）による配光分布の例と考え方 |
〔図−３〕楕円面鏡（回転楕円面）による配光分布
| * | 点光源の場合は一点に集光するが、現実の光源は面積を持つため点ではなくなる。この例は球状光源の場合。ミラーの奥で反射された光ほど大きな倍率で光源像がスクリーンに投射される。ミラー端部（開口端近く）で反射されたものは倍率が小さいので小さな光源像を作る。そしてそれらの光源像全てが合成されると、上図のように中心部が高く、周囲に裾野をもつ配光分布が得られる。 スクリーン上の光源像の径＝光源の径×（Ｌ2/Ｌ1） ------前項の解説参照 |
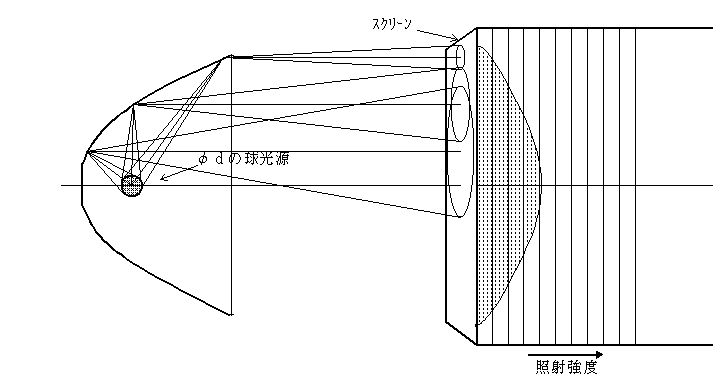
６．放物面鏡（パラボラ→平行光用）による配光分布の例と考え方 |
〔図−４〕放物面鏡（回転放物面−パラボラ）による配光分布
| * | 点光源の場合はミラー開口径に等しく、平坦な照度分布でスクリーンに照射されるが、現実の光源は必ず面積を持つため決して平行光などにはならず、また平坦な分布にもならない。必ず中央部が明るく周辺部が暗い配光となる。 ※ミラーの奥の方で反射された光は光源像が大きな倍率でスクリーンに投射され大きな光源像を 作る。 ※ミラー端部（開口端近く）で反射されたものは倍率が小さいので小さな光源像を作る。そしてそれ ら全ての光源像が合成されると、上図のように中心部の照度の高い山形配光分布となる。 |
７．均等な配光分布をもつミラー構造例と考え方 |
※微小ミラーで作られる光源像の端が、全て配光したい範囲の端にくるように設計されたミラーは、かなり
平坦な配光分布が得られ、かつ光の利用率が非常に良い。
８．ミラー座標の求め方 |
| * | ミラーは用途によって開口径が決まる事が多いが、先ずこれを決定する必要がある。これが決まると光源の位置を決める。通常は開口部からの距離が開口径の半分程度になるようにする。光源位置が深い方が光の利用率も一般的に高くなる。しかしミラー製作が困難になり、その他の不具合いも出てくる。 深いミラーはミラー周辺での微小ミラーの投射倍率が小さくなるので、楕円鏡で一点に集光させる場合には照射スポット径が小さくできる。だだしこれは狭い範囲に沢山の光が集められたわけではなく、中心部のパワー密度ピーク値はほとんど同じ。配光の山状カーブ（浅いミラーでは台形に近い）が崩れて山頂部が小さくなった（富士山形）だけと考えるべき。 開口径と光源位置が決まれば、開口端の一番端のミラーから角度を決めていく。決め方はスクリーン上のターゲットポイントに光源からの光が反射されるように角度を決定し、座標を求める。最初の微小ミラー座標がきまれば、それに連続するように次の微小ミラーの座標を求める。この作業をミラーの奥まで繰り返す。 ターゲットポイントの決め方は、現在のところ試行錯誤によっている。つまり適当と思われる位置にターゲットポイントを設定していき、取り合えずミラー全体の形を設計する。そしてそれがどのような配光分布になるかシミュレーションし、希望通りの配光でなければ微調整を加えていくという方法。この作業もコンピュータで完全自動化することはできるが、因果関係がやや複雑（ある配光を得るミラー形状の解は複数ある）なので簡単ではないのと、そこまでの必要を感じないので行っていない。 |
９．試作による評価 |
| * | ＮＣ旋盤を使って前記設計で決定した座標から回転多面体の形でミラーを削りだす。そしてバフ研磨し、研磨材を使って鏡面に仕上げれば配光の評価ができる。 |
| −参考− 以下はこのミラー設計方法により作ったパソコン用ソフトを使っての設計例です。外径約φ30のミラーを使い、30mm離れた位置をφ30の範囲で均等に加熱する、というのが設計目標です。 |
下図は前記入力を元にミラー設計をした結果のシミュレーションであり、平坦な配
光になるように設計しています。
ある範囲を目的の照度分布になるように照射させる場合ですが、光路を普通に目標
に向かわせる方式と、いったん光軸中心とクロスしてから目標に向かわせるやり方
があります。後者の方がミラーが深くなり、光の利用率が良くなります。ただし照
射距離を変化させた場合の照射範囲の変化は大きくなります。しかし照明用などは
照射距離が非常に長い（数ｍ）のが普通なので、その場合は差は少なくなり、クロ
スさせる方式が普通です。
以下の設計例ではクロスさせる方式を採用しています。
この設計によるミラー製作データです。x(n)とy(n)の座標データがあれば作れ
ます。
設計作業中に必要な情報です。下側の図は各微小ミラーが配光する範囲を示し
ています。
スクリーンを20mm移動させたときの配光シミュレーションです。このようにスク
リーンを移動させたり、光源位置を移動させたりした時の配光変化が簡単にシミ
ュレーション可能です。
以下はWindowsバージョンです。
Ｆｉｎｔｅｃｈ.ｃｏ.ｊｐ